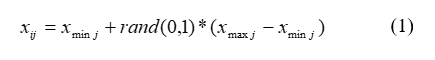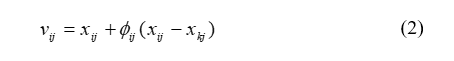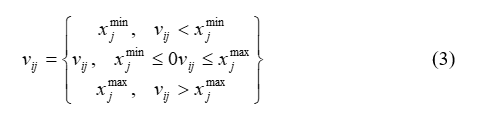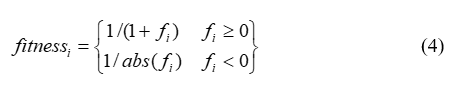Giriş
Bu yazıda önce Yapay Arı Koloni Algoritmasının (Artificial Bee Colony – ABC) temelini teşkil eden gerçek arıların yiyecek arama davranışı açıklanacaktır. Sonra yapay arı algoritması ve bu algoritmanın örnek bir problem için uygulamada kullanılması gösterilecektir.
Gerçek Arıların Davranışları
Doğal bir arı kolonisinde yapılacak işler o iş için özelleşmiş arılar tarafından yapılır. Yani yapılacak işlere göre arılar arasında bir iş bölümü vardır ve kendi kendilerine organize olabilmektedirler. İş bölümü yapabilme ve kendi kendine organize sürü zekâsının iki önemli bileşenidir. Arıların minimal yiyecek arama modelinde temel üç bileşen vardır. Bunlar; yiyecek kaynakları, görevli işçi arılar ve görevsiz işçi arılar.
Yiyecek kaynakları
Arıların nektar, polen veya bal elde etmek için gittikleri kaynaklardır. Kaynağın değeri, çeşidi, yuvaya yakınlığı, nektar konsantrasyonu veya nektarın çıkarılmasının kolaylığı birçok etkene bağlı olabilir. Ama kaynağın zenginliği tek ölçüt olarak alınabilir.
Görevli İşçi Arılar
Daha önceden keşfedilen belli kaynaklara ait nektarın kovana getirilmesinden sorumludur. Ayrıca ziyaret ettikleri kaynağın kalitesi ve yeri ile ilgili bilgiyi kovanda bekleyen diğer arılarla da paylaşırlar.
Görevsiz İşçi Arılar
Nektarın toplanacağı kaynak arayışı içerisindeki arılardır. Görevi belirsiz iki çeşit işçi arı bulunmaktadır. Bunlar; rastgele kaynak arayışında olan kâşif arılar ve kovanda bekleyen ve görevli arıları izleyerek bu arılar tarafından paylaşılan bilgiyi kullanarak yeni kaynağa yönelen gözcü arılardır.
Görevli arıların yiyecek kalitesi ve yeri ile ilgili bilgi paylaşımı dans alanında olmaktadır. Bir arı dans ederken diğer arılar ona antenleri ile dokunur ve bulduğu kaynağın tadı ve kokusu ile ilgili bilgiyi alır.
Danslar
Kaynağın kovana olan mesafesine göre çeşitli danslar mevcuttur: dairesel dans, kuyruk dansı ve titreme dansı gibi.
Daire Dansı Belirlenen yiyecek kaynağının kovana olan uzaklığı maksimum 50-100 metre civarında olduğundan bu dans yön ve uzaklık bilgisi içermez.
Titreme Dansı Arıların petek üzerinde düzensiz tarzda ve yavaş tempoda bacaklarını titreterek ileri, geri, sağa ve sola hareketleri söz konusudur. Arı zengin bir nektar kaynağı bulduğunu ancak kovana işlenebileceğinden fazla nektar geldiğini ve bundan dolayı nektar işleme görevine geçmek istediğini belirtmektedir. Bu dansın amacı kovan kapasitesi ve yiyecek getirme aktivitesi arasındaki dengeyi sağlamaktır.
Kuyruk Dansı 100 metreden 10 kilometreye kadar olan geniş bir alan içerisinde bulunan kaynaklarla ilgili bilgi aktarımında kullanılır. Bu dans 8 rakamına benzeyen figürlerin yapıldığı dans çeşididir. Dansı izleyen arıların bir titreşim oluşturması ile dansa son verilir. Dansın her 15 saniyede tekrarlanma sayısı, nektar kaynağının uzaklığı hakkında bilgi vermektedir. Daha az tekrarlanma sayısı daha uzak bölgeleri ifade etmektedir.
Yön bilgisi Şekil-1’deki gibi 8 rakamı şeklindeki dansın açı bilgisinden elde edilir. Şekilde verilen örnekte dansı izleyen arılar, danstan güneşle yiyecek arasındaki açının 45o olduğunu anlamaktadırlar.

Şekil-1 Arılarda Dans
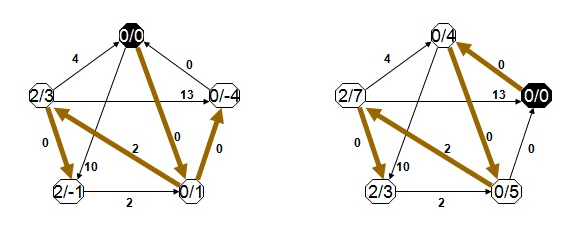
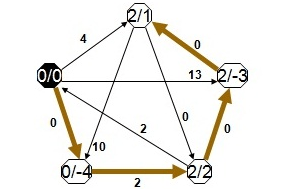
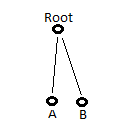
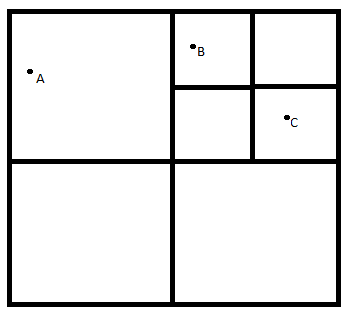
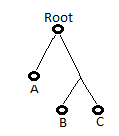
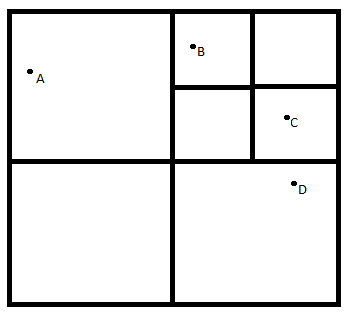
Tüm zengin kaynaklarla ilgili bilgiler dans alanında gözcü arılara iletildiğinden, gözcü arılar birkaç dansı izledikten sonra hangisini tercih edeceğine karar verir. Yiyecek arayıcı arıların daha iyi anlaşılabilmesi için Şekil-2’deki verilen modelin incelenmesi faydalı olacaktır.
A ve B ile gösterilen iki keşfedilmiş kayna bölgesi olduğunu varsayılım. Araştırma başlangıcında potansiyel yiyecek arayıcı, görevi belirsiz bir işçi arı olarak araştırmaya başlayacak ve bu arı kovan etrafındaki kaynakların yerinden haberdar degildir. Bu durumdaki arı için iki olası durum söz konusudur.
- Bu arı kaşif arı olabilir ve içsel ve dışsal etkilere bağlı olarak yiyecek aramaya başlayabilir (Şekil-2’de S ile gösterilmiştir).
- Bu arı kuyruk dansını izleyen gözcü arı olabilir ve izlediği dansla anlatılan kaynağa gidebilir (Şekil-2’de R ile gösterilmektedir). Bir kaynak keşfedildikten sonra arı imkanları dahilinde bu kaynağın yerini hafızaya alır ve hemen nektar toplamaya başlar. Bu arı artık nektarın zenginliğine göre görevli arı haline gelmiş olur. İşçi arı nektarı aldıktan sonra kovana döner ve bunu yiyecek depolayıcılara aktarır. Nektar aktarıldıktan sonra arı için üç seçenek ortaya çıkmaktadır:
- Gittiği kaynağı bırakarak bağımsız işçi olabilir (Şekil-2’de UF ile gösterilmiştir).
- Gittiği kaynağa dönmeden önce dans eder ve kovandaki arkadaşlarını da aynı kaynağa yönlendirebilir ( Şekil-2’de EF1 ile gösterilmiştir).
- Diger arıları yönlendirmeden direkt kaynağa gidebilir (Şekil-2’de EF2 ile gösterilmiştir).
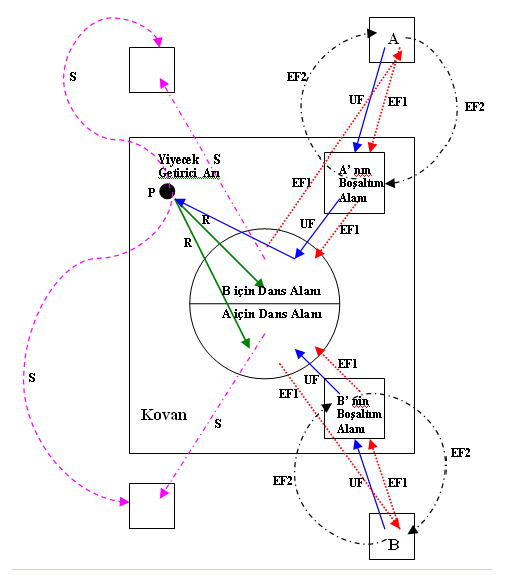
Şekil-2 Yiyecek Arama Çevrimi
Yapay Arı Kolonisi Algoritması
Doğada var olan zeki davranışlar içeren süreçlerin incelenmesi araştırmacıları yeni optimizasyon metotları geliştirmeye sevk etmiştir. Derviş Karaboğa, arıların yiyecek arama davranışını modelleyerek Yapay Arı Kolonisi(ABC) algoritması geliştirilmiştir.
Derviş Karaboğa’nın ABC algoritmasının temel aldığı modelde bazı kabuller yapılmaktadır. Bunlardan birincisi her bir kaynağın nektarının sadece bir görevli arı tarafından alınıyor olmasıdır. Yani görevli arıların sayısı toplam yiyecek kaynağı sayısına eşittir. İşçi arıların sayısı aynı zamanda gözcü arıların sayısına eşittir. Nektarı tükenmiş kaynağın görevli arısı artık kâşif arı haline dönüşmektedir. Yiyecek kaynaklarının yerleri optimizasyon problemine ait olası çözümlere ve kaynakların nektar miktarları ise o kaynaklarla ilgili çözümlerin kalitesine (uygunluk) karşılık gelmektedir. Dolayısıyla ABC optimizasyon algoritması en fazla nektara sahip kaynağın yerini bulmaya çalışarak uzaydaki çözümlerden problemin minimumu yada maksimumunu veren noktayı bulmaya çalışmaktadır.
Bu Modele ait süreç adımları aşağıdaki gibi verilebilir.
- Yiyecek Arama surecinin başlangıcında, kaşif arılar çevrede rastgele arama yaparak yiyecek aramaya başlarlar.
- Yiyecek kaynakları bulunduktan sonra, kaşif arılar artık görevli arı olurlar ve buldukları kaynaklardan kovana nektar taşımaya başlarlar. Her bir görevli arı kovana donup getirdiği nektarı boşaltır ve bu noktadan sonra ya bulduğu kaynağa geri döner ya da kaynakla ilgili bilgiyi dans alanında sergilediği dans aracılığıyla kovanda bekleyen gözcü arılara iletir. Eğer faydalandığı kaynak tükenmiş ise görevli kaşif arı haline gelir ve yeni kaynak arayışına yönelir.
- Kovanda Bekleyen gözcü arılar zengin kaynakları işaret eden dansları izlerler ve yiyeceğin kalitesi ile orantılı olan dans frekansına bağlı olarak bir kaynağı tercih ederler.
ABC algoritmasının bu süreçleri ve temel adımları ise şu şekilde sıralanabilir;
- Başlangıç yiyecek kaynağı bölgelerinin üretilmesi
- Repeat
- İçi arıların yiyecek kaynağı bölgelerine gönderilmesi
- Olasılıksal seleksiyonda kullanılacak olasılık değerlerinin görevli arılardan gelen bilgiye göre hesaplanması
- Gözcü arıların olasılık değerlerine göre yiyecek kaynağı bölgesi seçmeleri
- Kaynağı bırakma kriteri:limit ve kaşif arı üretimi
- Until çevrim sayısı=Maksimum çevrim sayısı
Yiyecek arayan arılarda görülen zeki davranış ile bu davranışı simule eden ABC algoritmasının temel birimleri aşağıda açıklanmaktadır.
1.Başlangıç Yiyecek Kaynağı Bölgelerinin Üretilmesi
Arama uzayını yiyecek kaynaklarını içeren kovan çevresi olarak düşünürsek algoritma arama uzayındaki çözümlere karşılık gelen rastgele yiyecek kaynağı yerleri üreterek çalışmaya başlamaktadır. Rastgele yer üretme sureci her bir parametrelerinin alt ve üst sınırları arasında rastgele değer üreterek gerçeklenir (Eşitlik-1).
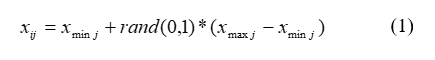
Burada i=1… SN, J=1…D ve SN yiyecek kaynağı sayısı ve D is optimize edilecek parametre sayısıdır. Xmin j parametrelerin alt sınırıdır.
2. İsçi Arıların Yiyecek Kaynağı Bölgelerine Gönderilmesi
Daha öncede belirtildiği gibi her bir kaynağın bir görevli arısı vardır. Dolayısıyla yiyecek kaynakların sayısı görevli arıların sayısına eşittir. İşçi arı çalıştığı yiyecek kaynağı komşuluğunda yeni bir yiyecek kaynağı belirler ve bunun kalitesini değerlendirir. Yeni kaynak daha iyi ise bu yeni kaynağı hafızasına alır. Yeni kaynağın mevcut kaynak komşuluğunda belirlenmesinin benzetimi Eşitlilik-2 tanımlanmaktadır.
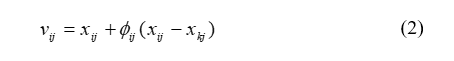
xi ile gösterilen her bir kaynak için bu kaynağın yani çözümünün tek bir parametresi (rastgele seçilen parametresi, j) değiştirilerek xi komşuluğunda vi kaynağı bulunur. Eşitlik 2 de j,[1,D] aralığında rastgele üretilen bir tamsayıdır. Rastgele seçilen j parametresi değiştirilirken, yine rastgele seçilen xk komsu çözümünün ( k E {1,2,SN} ) j. parametresi ile mevcut kaynağın j parametresinin farkları alınıp [-1 1 ] arasında rastgele değer alan sayısı ile ağırlandırıldıktan sonra mevcut kaynağın j parametresine eklenmektedir.
Eşitlik-2’den de görüldüğü gibi xi,j ve xk,j arasındaki fark azaldıkça yani çözümler birbirine benzedikçe xi,j parametresindeki değişim miktarı da azalacaktır. Böylece bölgesel optimal çözüme yaklaştıkça değişim miktarı da adaptif olarak azalacaktır.
Bu işlem sonucunda üretilen vi,j‘nin daha önceden belli olan parametre sınırları asması durumunda j. parametreye ait olan alt veya üst sınır değerlerine ötelenmektedir (Eşitlik-3).
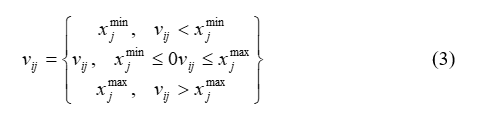
Sınırlar dâhilinde üretilen vi parametre vektörü yeni bir kaynağa temsil etmekte ve bunun kalitesi hesaplanarak bir uygunluk değeri atanmaktadır (Eşitlik-4).
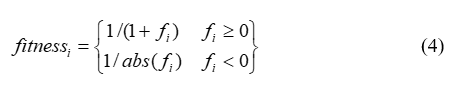
Burada fi ve vi kaynağının yani çözümünün maliyet değeridir. xi ve vi arasında nektar miktarlarına yani uygunluk değerlerine göre bir açgözlü (greddy) semce işlemi uygulanır. Yeni Bulunan vi çözümü daha iyi ise görevli arı hafızasından eski kaynağın yerini silerek vi kaynağının yerini hafızaya alır. Aksi takdirde görevli arı xi kaynağına gitmeye devam eder ve xi çözümü geliştirilemediği için xi kaynağı ile ilgili geliştirememe sayacı (failure) bir artar, geliştirdiği durumda ise sayaç sıfırlanır.
3. Gözcü Arıların Seleksiyonda Kullanacakları Olasılık Değerlerinin Hesaplanması (Dans Benzetimi)
Tüm görevli arılar bir çevrimde araştırmalarını tamamladıktan sonra kovana donup buldukları kaynakların nektar miktarları ile ilgili gözcü arılara bilgi aktarırlar. Bir gözcü arı dans aracılıyla paylaşılan bilgiden faydalanılarak yiyecek kaynaklarının nektar miktarları ile orantılı bir olasılıkla bir bölge(kaynak) seçer. Bu ABC‘nin altında çoklu etkileşim sergilendiğinin bir örneğidir. Olasılıksal seçme işlemi, algoritmada nektar miktarlarına karşılık gelen uygunluk değerleri uygulanarak yapılmaktadır. Uygunluk değerine bağlı seçme işlemi rulet tekerliği,sıralamaya dayalı, stokastik ,örnekleme, turnuva yöntemi yada diğer seleksiyon şemalarından herhangi biri ile gerçeklenir.Temel ABC algoritmasında bu seleksiyon işlemi rulet tekerliği kullanılarak yapılmıştır. Tekerlekteki her bir dilimin açısı uygunluk değeri toplamına oranı o kaynağın diğer kaynaklara göre nispi seçilme olasılığı olduğunu vermektedir (Eşitlik-5).

Burada kaynağın kalitesini SN görevli arı sayısını göstermektedir. Bu olasılık hesaplama işlemine göre bir kaynağın nektar miktarı arttıkça (uygunluk değeri arttıkça) bu kaynak bölgesini seçecek gözcü arı sayısı da artacaktır. Bu özellik ABC’ nin pozitif geri besleme özelliğine karşılık gelmektedir.
4. Gözcü Arıların Yiyecek Kaynağı Bölgesi Seçmeleri
Algoritma da olasılık değerleri hesaplandıktan sonra be değerler kullanılarak rulet tekerleğine göre secim işleminde her bir kaynak için [0.1] aralığında rastgele sayı üretilen ve pi değeri bu üretilen sayıdan büyükse görevli arılar gibi gözcü arı da Eşitlik-2’yi kullanarak bu kaynak bölgesinde yeni bir çözüm üretir. Yeni çözüm değerlendirilir ve kalitesi hesaplanır. Sonra yeni çözümle eski çözümün uygunluklarının karşılaştırıldığı en iyi olanın seçildiği açgözlü seleksiyon işlemine tabi tutulur. Yeni çözüm daha iyi ise eski çözüm yerine bu çözüm alınır ve çözüm geliştirememe sayacı (failure) sıfırlanır. Eski çözümün uygunluğu daha iyi ise bu çözüm muhafaza edilir ve geliştirememe sayacı (failure) bir artırılır. Bu süreç,tüm gözcü arılar yiyecek kaynağı bölgelerine dağılana kadar devam eder.
5. Kaynağı Bırakma Kriteri: Limit ve Kaşif Arı Üretimi
Bir çevrim sonunda tüm görevli ve gözcü arılar arama süreçlerini tamamladıktan sonra çözüm geliştirememe sayaçları (failure) kontrol edilir. Bir arının bir kayaktan faydalanıp faydalanmadığı, yani gidip geldiği kaynağın nektarının tükenip tükenmediği çözüm geliştirememe sayaçları aracılığıyla bilinir. Bir kaynak için çözüm geliştirememe sayacı belli bir eşik değerinin üzerindeyse, artık bu kaynağın görevli arısının tükenmiş olan o çözümü bırakıp kendisi için başka bir çözüm araması gerekir. Bu da biten kaynakla ilişkili olan görevli arının kâşif arı olması anlamına gelmektedir. Kâşif arı haline geldikten sonra, bu arı için rastgele çözüm arama sureci başlar (Eşitlik-1). Kaynağın terk ettiğinin belirlenmesi için kullanılan eşik değeri ABC algoritmasının önemli bir kontrol parametresidir ve “limit” olarak adlandırılmaktadır. Temel ABC algoritmasında her çevrimde sadece kâşif arının çıkmasına izin verilir.
Tüm bu birimler arasındaki ilişki ve döngü Şekil-3’deki gibi bir akış diyagramı ile şematize edilebilir.
6. Seleksiyon Mekanizmaları
ABC algoritması 4 farklı seleksiyon işlemi kullanmaktadır.Bunlar ;
- Potansiyel iyi kaynaklarının belirlenmesine yönelik eşitlik 5 olasılık değerlerinin hesaplandığı global olasılık temelli seleksiyon sureci.
- Görevli ve gözcü arıların renk,şekil,koku gibi nektar kaynağının turunu belirlenmesi sağlayan görsel bilgiyi kullanarak bir bölgede kaynağın bulunmasına vesile olan bölgesel olasılık tabanlı seleksiyon işlemi (Eşitlik-2).
- İşçi ve gözcü arıların daha iyi olan kaynağı belirlemek amacıyla kullandıkları açgözlü seleksiyon.
- Kâşif Arılar tarafından eşitlik 1 aracılıyla gerçekleştirilen rastgele seleksiyon.
Bütün bu seleksiyon metotların bir arada kullanılmasıyla ABC algoritması hem iyi bir global araştırma hem de bölgesel araştırma yapabilmektedir.
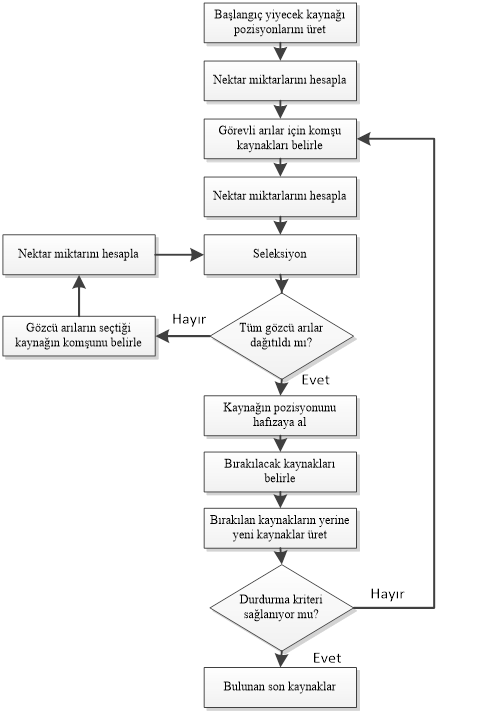
ABC Algoritması Akış Şeması
7. ABC Algoritmasının Adımları
Önceki bölümlerde genel hatları ile ABC algoritmasının adımları ve her bir adımda yapılan işlemler tarif edilmişti ancak bu adımları sözde kod seklinde baştan aşağı yazmak faydalı olacaktır.
- Eşitlik 1 aracılıyla tüm xi,j i=1…SN,j =1…D, çözümlerine başlangıç değerlerinin atanması ve çözüm geliştirememe sayaçlarının sıfırlanması failurei=0
- fi=f(xi) fonksiyon değerlerinin ve bu değerlere karşılık gelen uygunluk değerlerin hesaplaması
- Repeat
- for i=1 to Sn do
- Eşitlik 2 kullanarak xi çözümünün görevli arısı için yeni bir kaynak üret vi ve f(vi)’yi (4) eşitliğinde yerine koyarak bu çözümün uygunluk değerini hesapla
- xi ve vi arasında açgözlü seleksiyon işlemi uygula ve daha iyi olanı seç
- xi çözümü gelişememişse çözüm geliştireme sayacını bir artır failurei= failurei+1, gelişmemişse sıfırla, failurei=0
- End For
- Eşitlik 5 ile gözcü arıların seçim yaparken kullanacakları uygunluk değerine dayalı olasılık değerlerini pi hesapla
- t=0 i=1
- Repeat
- if random<pi then
- Eşitlik 2 ‘i kullanarak gözcü arı için yeni bir kaynak, vi üret
- xi ve vi arasında açgözlü seleksiyon işlemi uygula ve daha iyi olanı seç.
- xi çözümü gelişememişse çözüm geliştirememe sayacını bir artır failurei= failurei+1, gelişmemişse sıfırla, failurei=0
- t=t1
- End İf
- Until t=SN
- if max (failurei) > limit then
- xi eşitlik 1 ile üretilen rastgele bir çözümle değiştir.
- End İf
- En İyi Çözümü hafıza da tut
- Until Durma kriteri
ABC’nin Temel Özellikleri
ABC algoritmasının temel özellikleri şu şekilde sıralanabilir;
- Oldukça esnek ve basittir.
- Gerçek yiyecek arayıcı arıların davranışlarına oldukça yakın şekilde simule eder.
- Sürü zekâsına dayalı bir algoritmadır.
- Nümerik problemler için geliştirilmiştir ama ayrık problemler içinde kullanılabilir.
- Oldukça az kontrol parametresine sahiptir
- Kâşif Arılar tarafından gerçekleştirmen küresel ve görevli ve gözcü arılar tarafından gerçekleştirilen bölgesel araştırma kabiliyetine sahiptir ve ikisi paralel yürütülmektedir.
UYGULAMA VE DENEY SONUÇLARI
Algoritmanın performansını Rastrigin Problemi üzerinde görmeye çalıştık. Bu anlamda bu fonksiyonu çözmeye çalıştık. Deney sonuç ve performanslarına geçmeden önce Rastrigin Problemi ve Fonksiyonu nedir ve ne işe yarar bundan bahsetmek istiyorum. Rastrigin fonksiyonu içerisinde birçok lokal minimumu içeren ve bu yüzden de optimizasyon tekniklerinin performansını ölçmek için ideal olan bir test fonksiyonudur. Fonksiyonun global minimumu iki boyutlu uzay için [0,0] noktası, üç boyutlu bir uzay için ise [0,0,0] noktasıdır. Fonksiyonun grafik üzerindeki görünümü aşağıdaki şekildeki gibidir.

Kullandığım demo uygulama http://mf.erciyes.edu.tr/abc/ web sitesinden alınmıştır. Çeşitli optimizasyon problemleri üzerinde ABC Algoritması’ nın performansını gözlemektedir. Biz yukarıda da bahsettiğimiz üzere bu fonksiyonlardan Rastrigin Fonksiyonunu kullandık. Demo uygulamanın genel görünümü aşağıdaki gibidir.
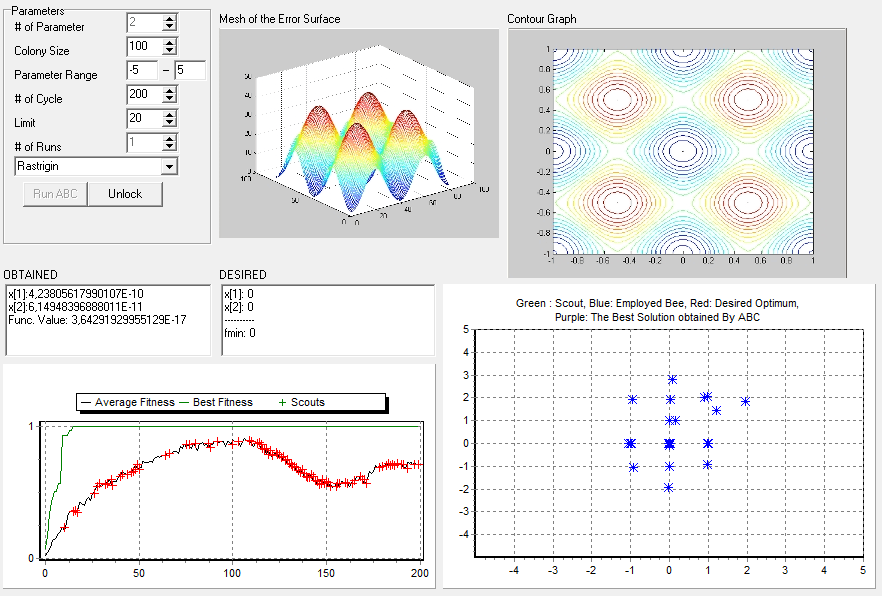
Öncelikle uygulamanın parametrelerine bakalım. Demo üzerinde parametreler ve açıklamaları aşağıda sırasıyla verilmiştir.
- # of parameter: Üzerinde çalışılan uzayın boyutu. Biz uygulamamızda anlaşılması ve gözlemi kolay olması maksadıyla 2 boyutlu uzayda çalışmayı tercih ettik.
- Colony Size: Kolonide bulunan arı miktarı.
- Parameter Range: Algoritmanın çalışmasını istediğimiz aralık. Yukarıdaki görülen şekilde aralık [-5,5] olarak seçilmiştir. Böylelikle alan daraltılarak arıların hareketi daha rahat görülmektedir.
- # of Cycle: Algoritmanın durdurma kriteri olarak çalışma sayısı belirtilmiştir.
- Limit: Her döngüde görevli ve gözcü arılar arama süreçlerini tamamladıktan sonra çözüm geliştirememe sayaçlarına bakarlar eğer ki limit değeri aşılmışsa yani algoritma belli bir süre boyunca artık iyi değer vermemeye başlamışsa bu bölgeden vazgeçilir. Limit değeri bu sayacı belirtmektedir.
- # of Runs: Algoritmanın baştan itibaren kaç defa çalışacağı. Biz her defasında varsayılan değer kabul edilen bir kez çalıştırdık.
Ayrıca demo şekil üzerinde görülen Obtained kısmı algoritmanın bulduğu en iyi değerleri, Desired kısmı fonksiyonun beklenilen değerlerini, üst soldaki grafik Rastrigin Fonksiyonu’nun grafiksel olarak üç boyutlu görünümünü, üst sağdaki grafik fonksiyon grafiğinin üstten görünümünü, sol alttaki grafik en iyi değerin kaçıncı döngüde bulunduğunu ve bulunan değerlerin ortalama iyiliğini göstermektedir. Sağ alttaki grafik ise arıların hareketini her döngüde izleme imkânı sunmaktadır. Buradaki mavi noktalar, görevli işçi arılar; yeşil noktalar, kaşif; kırmızı noktalar, beklenen değer; ve son olarak da mor noktalar, o ana kadar ki bulunan en iyi çözüm noktasını göstermektedir.
Deney Sonuçları: Yaptığımız deneylerde Colony Size, Cycle Sayısı ve Limit Sayısı parametrelerinin algoritmanın performansı üzerindeki etkilerine baktık. Her deney çeşidi için en az 5’er adet deney yapılmıştır.
Colony Size Deneyi
Sabit Değerler: Parameter Range (-5,5), Cycle (100), Limit (20)
- Deney Colony Size Değeri: 30
- Deney Colony Size Değeri: 50
- Deney Colony Size Değeri: 60
- Deney Colony Size Değeri: 75
- Deney Colony Size Değeri: 100
Deney Değerlendirmesi: Bulunan en iyi değerlere bakıldığında yaptığımız deney için Colony Size değişimi çok etki etmemiştir fakat Colony Size’ın artışı algoritmanın daha az döngüde en iyi değerlere ulaşmasını sağlamıştır. Yani koloni büyüklüğü problemin daha kısa sürede çözülmesini sağlamaktadır. Bu durumda eğer ki Colony Size’ı artırma imkânımız yoksa döngü (cycle) sayısının yüksek tutulması gerekir. Aksi takdirde en iyi çözüme çok yakın olan çözümlere ulaşamayabiliriz.
# of Cycle Deneyi (Döngü Sayısı)
Sabit Değerler: Colony Size(50), Parameter Range (-5,5), Limit (20)
- Deney Cycle Değeri: 10
- Deney Cycle Değeri: 20
- Deney Cycle Değeri: 50
- Deney Cycle Değeri: 70
- Deney Cycle Değeri: 100
Deney Değerlendirmesi: Colony Size deneyinde 10 ile 100 döngü arasında deneyler yaptık. 10 beklenen değerler için çok bir sayı oldu ve hata oranı çok fazla çıktı. Belirlenen parametrelerde için bu deneyde cycle değerini artırmaya başladık ilk anlamlı sonuç 20’de çıkmıştır ve beklenen değere yüzde bir oranında hataya sahip değerler bulunmuştur. Bundan sonraki artışlar hata oranını giderek düşürmeye başlamış fakat yaklaşık 70 cycle’dan sonra hata oranında çok fazla bir değişim olmamaya başlamıştır. Belirlenen sabit parametrelere göre bu deney için yaklaşık 70 cycle değeri uygun bir değer olarak belirlenmiştir. Cycle değeri belli bir yere kadar olumlu etki etmekte, belli bir yerden sonra ise etmemektedir.
# Limit Deneyi
Sabit Değerler: Colony Size(50), Parameter Range (-5,5), Cycle(80)
- Deney Limit Değeri: 5
- Deney Limit Değeri: 10
- Deney Limit Değeri: 20
- Deney Limit Değeri: 40
- Deney Limit Değeri: 50
- Deney Limit Değeri: 60
- Deney Limit Değeri: 70
Deney Değerlendirmesi: Limit deneyinde diğer parametreler sabit kalmak koşuluyla limit değeri olarak 5’ten 70’e kadar deneyler yaptık. 5 değerinde yüksek cycle değerlerinde beklenen değere yakın değerler elde ettik. Limit değerini artırmaya başladık ve yavaş yavaş daha az cycle’da beklenen değerlere çok yakın değerler elde etmeye başladık. Fakat sabit değerlerle birlikte yaklaşık 20 limit değerinden sonraki değerlerde çok tutarlı sonuçlar elde edemedir. Yani 20 için daha az iken, 40 ta cycle değeri arttı, ama 50’de yine azaldı. Bu deneyler sonucunda limit değerinin cycle sayısına göre ayarlanması gerektiğiniz düşünüyoruz. Çünkü bu deneyde cycle 80 iken limit değerini 70’e kadar artırdık. Belli bir noktadan sonra anlamsız sonuçlar elde ettik. Bu sebeple limit için bizim düşüncemiz cycle sayısının yaklaşık yüzde 10’u ile %25’i arasında bir değer alması ideal olacaktır.
KAYNAKLAR


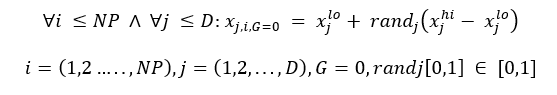 3. Değerlendirme Fonksiyonu
3. Değerlendirme Fonksiyonu 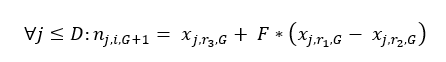 5. Rekombinasyon İşlemi
5. Rekombinasyon İşlemi  6. Seleksiyon İşlemi
6. Seleksiyon İşlemi