Kuyruk teorisi ve sistemlerini anlamak için öncelikle kuyruk (queue) ne demek ona bakmalıyız. Kuyruk hizmet kapasitesinin aşılması durumunda ortaya çıkan bekleme durumudur. Süper market kuyruğu gerçek hayattan verilebilecek en güzel örneklerden biridir. Banka sıramatiklerinden sıra alarak sırasını bekleyen müşteriler de güzel bir örnek olabilir. Bilgisayar sistemlerinden örnek olarak da yazıcı kuyruğu verilebilir. Bilindiği üzere ortak bir yazıcıya çıktı gönderen kişilerden çıktıyı ilk alacak olan ilk gönderen kişidir. Verilen örneklerdeki esas olan konu herkesin sırasını beklemesidir. İdeal olan ve istenilen beklemenin olmamasıdır, fakat bu mümkün görünmemektedir. Bu durumda yapılacak olan şey bu süreyi minimize etmektir. Çünkü kuyruğa farklı bir açıdan bakıldığında kuyruğun başlama sebebi hizmet kapasitesinin aşılması durumunda ortaya çıkmaktadır.
Şu ana kadar verdiğimiz örneklerin tarzı ilk giren ilk çıkar (first in first out) mantığı ile çalışan sistemlerdi. Bunun dışında restoran örneğine bakacak olursak, yoğun çalışan bir restoranda her zaman ilk gelen ilk çıkmadığı gibi bekleme süresi de değişebilmektedir. Ayrıca yemek tercihine göre servis süresi de değişken olacaktır. Yani burada durum biraz daha karışıktır. Bu durumda restoran sahibi hizmet maliyeti ve müşteri bekleme süresinin az, kalitenin ise fazla olmasını amaçlar. Müşteri için ise zaman ve hizmet kalitesi önemlidir. Bu durumda müşteri ve işletme sahibinin isteklerini dengeleyen bir yapının modeli kuyruk analizi ile çıkarılabilir. Kuyruk teorisi bekleyen sıra ya da kuyrukların matematiksel analizinin yapılarak bekleme süresini minimize edilmesine çalışılmasıdır. Kuyruk ya da sıralı sistemlerde temel elemanlar müşteri ve hizmet verendir.
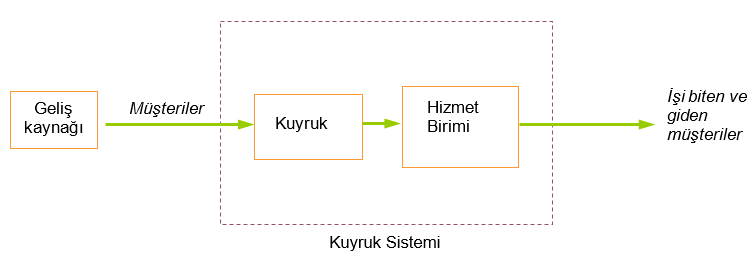
Kuyruk teorisinin temel kavramları şunlardır;
- Kuyruk: Bekleyen müşteri sayısı
- Servis Kanalı: Hizmet sunulan sistem
- Geliş Debisi (λ): Birim zamanda kuyruğa gelen müşteri sayısı
- Servis Debisi (μ): Birim zamanda hizmet verilen müşteri sayısı
- Kuyruk Disiplini: Müşterilerin seçilme düzeni. (Yazıcı ya da süper market kuyruğunda ilk gelen ilk çıkar mantığı olduğu gibi farklı sistemlerde ilk gelen son çıkar ya da rasgele seçilim gibi farklı disiplinler kullanılabilir.)
- Servis Olanaklarının Yapısı: Tek kanallı ya da çok kanallı bir yapı olabilir.
Tek kuyruk – tek servis düzeni, tek kuyruk – seri şekilde birden fazla servis, tek kuyruk – paralel şekilde servis, çoklu kuyruk – paralel şekilde çoklu servisi sistemleri kullanılabilecek olan kuyruk sistemlerindendir.
Daha önce de bahsedildiği üzere farklı kuyruk yapıları mevcuttur. Bunlardan M/M/1 Servis zamanının üstel olasılık dağılımına sahip olduğu, FIFO yapısı kullanılan, kuyruk kapasitesi sonsuz, matematiksel çözümü olan bir modeldir. Müşterilerin geliş sırası net olarak bilinemediği için buralarda poisson ve üstel olasılık dağılımları kullanılabilir. Modelleme için kullanılan değişkenlere ve bunların denklemlerine bakalım;
- Sistemin meşguliyet faktörü: ρ
- Verilen bir zamanda sistemde n sayıda müşteri bulunma olasılığı: Pn = (1 – ρ) ρn
- Hizmet verenin boş kalma oranı: Po = 1- ρ
- Sistemde n veya daha fazla birimin bulunma olasılığı: ρn
- Sistemdeki ortalama müşteri sayısı: L = ρ / (1- ρ)
- Müşterinin harcadığı süre: W = 1 / ( μ- λ )
- Ortalama Kuyruk Uzunluğu: Lq = λ2 / μ ( μ- λ )
- Müşterilerin kuyrukta geçirdiği ortalama süre: Wq = ρ / ( μ- λ ) (FIFO)
Farklı kuyruk yapıları gelişlerin dağılımının, hizmet süresinin dağılımının, kuyruk boyutunun, müşteri sayısının vb. kavramların farklı kombinasyonlarıyla hazırlanmıştır. Buna göre M/M/1’in dışında M/M/k, M/M/3, M/G/1 modelleri bulunmaktadır.
Farklı kuyruk yapıları gelişlerin dağılımının, hizmet süresinin dağılımının, kuyruk boyutunun, müşteri sayısının vb. kavramların farklı kombinasyonlarıyla hazırlanmıştır. Buna göre M/M/1’in dışında M/M/k, M/M/3, M/G/1 modelleri bulunmaktadır.
Kaynaklar
- http://tr.wikipedia.org
- http://www.ozyazilim.com
- gazi.edu.tr
- http://acikders.ankara.edu.tr/
- baskent.edu.tr
- trakya.edu.tr https://www.google.com.tr/url?sa=t&rct=j&q=&esrc=s&source=web&cd=2&ved=0CDEQFjAB&url=http%3A%2F%2Fozlemaydin.trakya.edu.tr%2FMod_2012_5.pptx&ei=hFOnUeraMci0PPaQgbgF&usg=AFQjCNENwsCS7NFd-TqaBi63LYljMP6b1g&sig2=PtYiOayQjBJAS0j9J0A-Fw&bvm=bv.47244034,d.ZWU&cad=rja