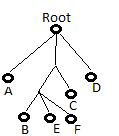
Lisans döneminde algoritma ödevlerimizden bir tanesi girilen takım sayısına göre fikstür oluşturan bir programdı. Aklıma gelince paylaşayım istedim.
ÇİFT SAYIDA TAKIM İLE FİKSTÜR OLUŞTURMA
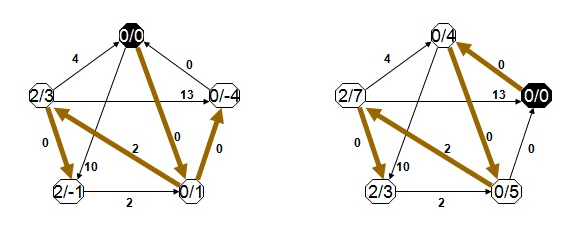
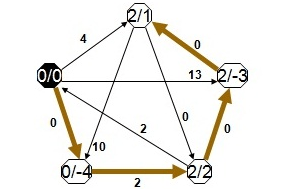
Fikstür algoritmalarında mantık; n adet takım varsa, ligde n-1 adet hafta müsabaka olmalıdır. (Rövanşlar hesaba katılırsa hafta sayısı 2 x (n-1) olacaktır.) İlk haftanın fikstürü çekilir, diğer haftalar ise ilk hafta referans alınarak belirlenir. Bizim kullandığımız algoritmayı örnekle açıklayayım. Örneğin 6 takımlı bir lig oluşturalım. Bu takımları 1, 2, 3, 4, 5, 6 şeklinde ifade edelim. İlk hafta maçları şu şekilde olsun;
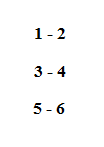
Birinci haftayı oluşturduktan sonra ilk takımı sabit tutarak diğer takımları saat yönünün tersinde ilerletelim. Bu durumda ikinci hafta aşağıdaki şekilde olacaktır;
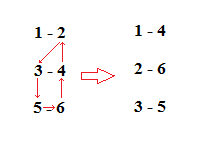
İlk takımı sabit tutup diğer haftaları bu şekilde hesaplamaya devam ettiğimiz taktirde 6 takımlı ligin 5 hafta sürecek müsabakalarının fikstürü aşağıdaki gibi olacaktır.

Fikstür bu şekilde belirlendikten sonra ev – deplasman ayarları da yapılabilir.
TEK SAYIDA TAKIM İLE FİKSTÜR OLUŞTURMA
Farklı bir durum da tek sayıda takım olması durumudur. Bu durumda ilk hafta oluşturulurken bir takımın karşısına X yazılabilir. Böylelikle fikstür çekimi sonucunda karşısına X gelen takım o haftayı bay geçecektir.
Her iki durum için de fikstür ayarlaması yukarıdaki gibi yapıldıktan sonra rasgele her takım için bir sayı çekilir. Örneğin Galatasaray geldi kura çekti ve 2 çıktı, Fenerbahçe’ye 3 çıktı vs. Bu durumda her sayıya karşılık gelen takım belirlenmiş olur.
ALGORİTMA
Bazı talepler üzerine algoritmanın kabakoduyla alakalı biraz daha bilgi vermek istedim.
N adet takım olsun. Öncelikle takımları bir diziye attım. N-1 hafta maç olmalı (deplasmanları saymazsak, sayacaksak eğer fikstürün tam tersi olacak zaten).Örnekte olduğu gibi 6 tane takım olsun (mantığını kavrayınca istenirse 500 olsun sorun yok). Tüm takımları bir diziye atalım. Daha sonra random olarak bir indis seçip sabit tutacağımız takımı belirleyelim ve o indisi diziden silelim. Bu durumda bir takım seçtik ve 5 adet takım dizide kaldı. Takım isimleri de 1, 2, 3, 4, 5 ve 6 olsun. Biz 1’i sabit seçmiş olalım. Bu durumda;sabit takım – 1takım_dizisi = [2, 3, 5, 6, 4]sabit takım ile dizinin ilk elemanı eşleşecek, kalan takımlar ise dışarıdan içeriye doğru eşleşecekler (bu örnek için dizinin ikinci elemanı (3) ile beşinci (6), üçüncü elemanı (4) ile dördüncü elemanı (5)). Yani;1-2, 3-4, 5-6Sonra dizideki elemanları bir kaydırıyoruz. Yeni dizimiz şöyle olacak;takım_dizisi = [4, 2, 3, 5, 6]kural yine aynı sabit ile dizinin ilk elemanı eşleşecek, kalan takımlar ise dışarıdan içeriye doğru eşleşecekler. Yani;1-4, 2-6, 3,5Sonra dizideki elemanları bir kaydırıyoruz. Yeni dizimiş şöyle olacak;takım_dizisi = [6, 4, 2, 3, 5]kural yine aynı sabit ile dizinin ilk elemanı eşleşecek, kalan takımlar ise dışarıdan içeriye doğru eşleşecekler. Yani;1-6, 4-5, 2-3Sonra dizideki elemanları bir kaydırıyoruz. Yeni dizimiş şöyle olacak;takım_dizisi = [5, 6, 4, 2, 3]kural yine aynı sabit ile dizinin ilk elemanı eşleşecek, kalan takımlar ise dışarıdan içeriye doğru eşleşecekler. Yani;1-5, 6-3, 4-2Sonra dizideki elemanları bir kaydırıyoruz. Yeni dizimiş şöyle olacak;takım_dizisi = [3, 5, 6, 4, 2]kural yine aynı sabit ile dizinin ilk elemanı eşleşecek, kalan takımlar ise dışarıdan içeriye doğru eşleşecekler. Yani;1-3, 5-2, 6-4Böylelikle 6 takım olduğu için 5 haftalık fikstür tamamlanmış oluyor.Kısaca algoritma şu;n tane takım için takımların hepsini diziye at. Bir tane random takım belirle ve sabit takım olarak seç. Bu takımı diziden sil.indis = random (1,n)sabit_takim = dizi(indis)dizi.pop(indis)for i = 1 to (n-1)i. hafta fikstur =1. maç = sabit_takim:dizi(0)for j=1 to (n-2)/2:j. maç = dizi(j+1):dizi(n-j)
Fikstür çekme ile ilgili sorunuz olursa bu yazıya yorum yazarak sorabilir veya mail atabilirsiniz. Bu yazı işinize yaramışsa veya hoşunuza gitmişse sayfadaki reklamlara tıklayarak teşekkür edebilirsiniz. 🙂