En Kısa Yol Problemi’nden (The Shortest Path Problem) daha önce bahsetmiştim. Bu yazımda bu problemi çözmek için kullanılan algoritmalardan kısaca bahsedip, Johnson Algoritması’nın üzerinde duracağım. En Kısa Yol Problemi için üretilen algoritmaların bazıları şunlardır;
- Djikstra Algoritması
- Bellman Ford Algoritması
- Floyd – Warshall Algoritması
- Johnson Algoritması
- A* Search Algoritması
- Dinitz Algoritması
- Tarjan Algoritması
- GOR Algoritması
- Dial Algoritması
Algoritmalardan bazılarına kısaca göz atacak olursak;
- Dijkstra Algoritması: Single Source, Single Pair ve Single Destination problemlerini çözmek için kullanılır. Döngüye girme ihtimalinden dolayı negatif ağırlıklı bağlantıları kabul etmez. Basit bir algoritmadır. Buna karşı performansı yüksektir.
- Bellman Ford Algoritması: Single Source problemlerini kenar ağırlıkları negatif olduğu durumlarda da çözebilmektedir.
- A* Search Algoritması: İki nokta arasındaki en kısa yolu aramayı hızlandırmak için sezgisel yöntemler kullanarak çözüm arar.
- Floyd – Warshall Algoritması : All pairs probleminin çözümünde kullanılır.
- Johnson Algoritması : Floyd Warshall Algoritması’ndaki gibi all pairs problemini çözmeye yarar. Sparse(dağınık) ve yönlü graflar için kullanılan bir algoritmadır. Sparse graflarda Floyd-Warshall’dan daha hızlı çalışır. Daha yoğun grafiklerde daha hızlı çalışabilir.En önemli özelliği negatif kenarlar içeren graflar için çözüm sunar.
Johnson Algoritması (Johnson’s Algorithm)
1977 yılında Donald B. Johnson tarafından geliştirilmiştir. Bellman Ford, Reweighting ve Dijkstra Algoritması tabanlı, All pairs problemini çözmek için kullanılan bir algoritmadır. Sparse(dağınık) ve directed(yönlü) graflar için kullanılan güzel bir çözüm yoludur. Bağlantıların negatif olmasına izin vermektedir ve bu en önemli özelliğidir. Negatif bağlantıları reweighting yöntemiyle işlem sırasında ağırlıkları yeniden hesaplayarak pozitif ağırlıklara güncellemektedir. Bu yönüyle Floyd Warshall’a benzemektedir fakat O(V3) olan çalışma süresi Johnson Algoritması’nın tercih edilmesine neden olur. Ayrıca Floyd Marshall daha sık graflarda tercih edilirken, Johnson seyrek graflarda daha iyidir. Ağırlıkların pozitif olması durumunda Dijkstra’nın kullanılması daha iyi performans sağlar. Algoritmanın adımlarını aşağıdaki graf üzerinde açıklayalım.
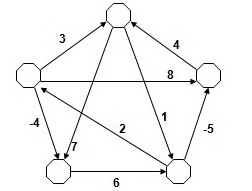
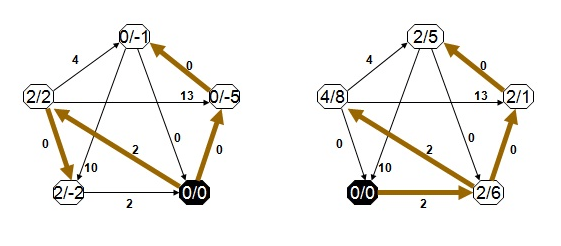
- Adım 1: Öncelikle grafa aşağıda görüldüğü üzere yeni bir düğüm ve bu düğümden grafta bulunan tüm düğümlere bağlantılar eklenir. Bu düğümün ve bağlantılarının ağırlığı sıfır olarak belirlenir.
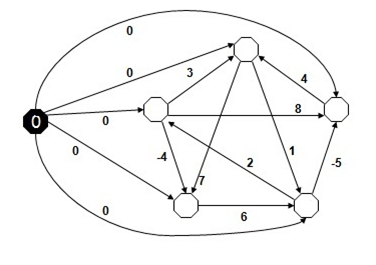
- Adım 2: Her düğüm için Bellman–Ford Algoritması bir kez çalıştırılır ve düğümlerin ağırlıkları belirlenir. Aşağıda görüldüğü üzere her düğümün ağırlığı içerisine yazıldı.
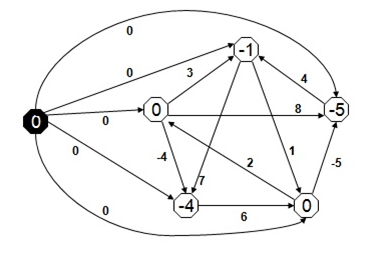
- Adım 3 : Adım 4’te Dijkstra Algoritması kullanılacaktır. Bilindiği üzere Dijkstra Algoritması negatif bağlantı uzunluklarını kabul etmemektedir. Bu yüzden bu adımda ağırlıklar tekrar hesaplama yöntemiyle yenilecek ve negatif bağlantı kalmayacaktır. Yeniden hesaplama yöntemi şu şekildedir; ŵ(u, v) = w(u, v) + d(s, u) – d(s, v)
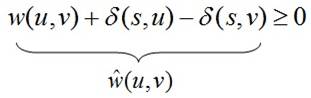
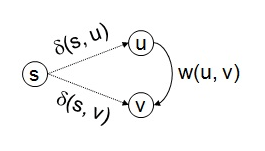
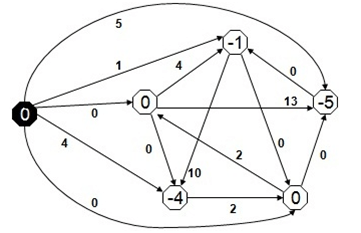
Ağırlıkların yeniden hesaplanması Reweighting Teorem ile yapılır. Formülde yeni kenar ağırlığı eski kenar ağırlığı ile düğümün, algoritmanın birinci adımında eklenen yeni düğümüne olan ağırlığı ile toplanır. Bu değerden gidilecek olan düğümün S düğümüne olan ağırlığı çıkarılır ve yeni ağırlık bulunur. Reweightin işlemi sonucunda shortest path değişmezken, ağırlıkların hepsi nonnegative olur. Burada akla şu soru gelebilir; ağırlıkları bu şekilde hesaplayacağımıza tüm düğümlere minimum bağlantı uzunluğunu eklesek olmazmı? Olmaz çünkü bu en kısa yolun değişmesine sebep olabilir. Aşağıda ağırlıkların güncellenmiş hali bulunmaktadır. Kenarların yeni ağırlıklarının bulunma işlemine örnek verecek olursak ; eski ağırlığı 8 olan kenarın yeni ağırlığı yukarıda bahsettiğimiz yöntemle 8 + 0 – (-5) = 13 ‘e olarak hesaplanır.
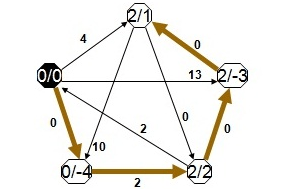
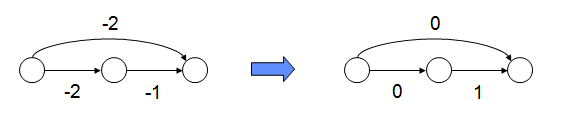
Aşağıdaki grafikta tüm düğümlere minimum düğüm ağırlığının eklenmesi durumunda ortaya çıkacak bozulma görülmektedir. Birinci durumda kısa yol alttaki iken, ikinci durumda üstteki oluyor. Bu metod görüldüğü üzere kısa yolun değişmesine sebep oluyor.
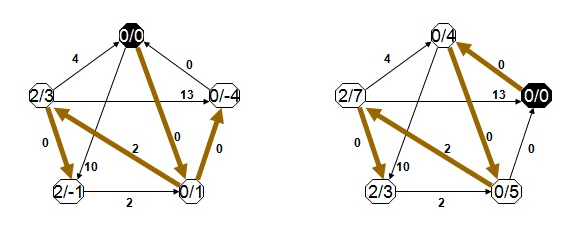
- Adım 4 : Birinci adımda eklenen düğüm graftan silinir ve geri kalan tüm düğümler için Dijkstra Algoritması uygulanır. Tüm çiftler arası en kısa yol bulunur. Aşağıda tüm düğümler için ağırlıkların Dijkstra Algoritması’yla yeniden hesaplanması görülmektedir.
ALGORİTMANIN KARMAŞIKLIĞI
Algoritmanın karmaşıklığına bakalım. Algoritmanın adımlarını kontrol edelim.
- İlk adımda yeni düğüm ekleniyor ve her düğümün ağırlığı Bellman Ford ile hesaplanıyor. Bu durumun getirdiği karmaşıklık O(VE)’dir.
- Daha sonra negatif kenarlardan kurtarmak için reweighting işlemi yapılıyor. Bu durumun getirdiği karmaşıklık O(E)’dir.
- Her düğüm için Djikstra Algoritması’nın getirdiği karmaşıklık O(V2 logV + VE logV )’dir.
Bu durumda Johnson Algoritması’nın karmaşıklığı O(V2 logV + VE logV) olarak hesaplanır.
(V: Düğümler Kümesi , E: Bağlantılar Kümesi )
Kaynaklar
- Tr.wikipedia.org
- http://en.wikipedia.org/wiki/Johnson’s_algorithm
- http://e-bergi.com/2009/Ekim/En-Kisa-Yol-Algoritmasi
- http://www.caveshadow.com/CS566/Chang-Ju%20Lin%20-%20Johnson’s%20Algorithm.ppt
- ceng.gazi.edu.tr/~akcayol/files/AAL12Greedy2.pdf
- www.gyte.edu.tr The shortest path problem ppt