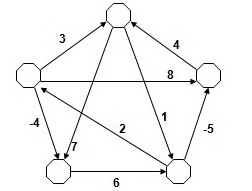
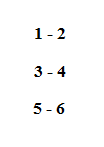Parçacık Sürüsü Optimizasyon Algoritması(PSO), kuş sürülerinin davranışlarından esinlenilerek ortaya çıkarılmış bir algoritmadır. Popülasyon tabanlıdır ve skotastik bir yapıya sahiptir. Sosyal sistemler bireyin çevresiyle ve diğer bireylerle olan etkileşimini ve davranışını incelemektedir. Bu davranışlara sürü zekası denmektedir. Sürülerden esinlenilerek ortaya çıkarılan iki popüler optimizasyon yöntemi vardır. Bunlar; Karınca Koloni Optimizasyonu ve Parçacık Sürü Optimizasyonudur.PSO sürünün besin kaynağı ararken ortaya koyduğu davranış üzerine kuruludur. PSO, evrimsel algoritmalarla bir çok benzerlik göstermektedir. PSO’nun adımları aşağıdaki gibidir. taşıma şirketi

Algoritmada bahsedilen parçacıklar sürüdeki bireylere işaret etmektedir.
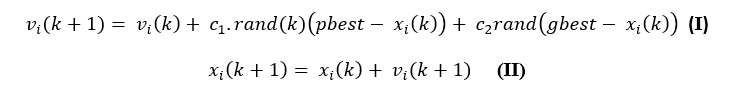
PSO KONTROL PARAMETRELERİ
- Parçacık Sayısı : Problemin çeşidine göre ayarlanmalıdır. Bazı problemlerde 10 parçacık yeterliyken, bazılarında 20-40, bazılarında ise 100-200 değerleri gerekmektedir.
- Parçacık Boyutu : Optimize edilecek probleme göre değişir.
- Parçacık Aralığı :Probleme göre farklı boyut ve aralıklarda ayarlanabilir.
- Vmax : Bir iterasyonda bir parçacıkta meydana gelecek maksimum hızı belirler. Genellikle parçacık aralığına göre ayarlanır.
- Öğrenme Faktörleri : Denklemde görülen c değerleridir. Genellikle 2 olarak seçilirler. Fakat farklı değerler de alabilirler. Yaygın olarak [0,4] aralığında alınır.
- Durdurma Kriteri : İki şekilde yapılabilir; Birincisi başlangıçta maksimum iterasyon sayısı belirlenir ve algoritma bu sayıya ulaştığında sonlandırılır. İkincisi ise değerlendirme fonksiyonu istenilen değere ulaştığından algoritma sonlandırılır.
Algoritmanın Pseudo Code’u aşağıdaki gibidir.
Begin
While Durdurma kriteri sağlanmıyorsa do
Begin
for i = 1 to parçacık sayısı
Uygunluk Değeri := f(Xi);
Pi ve gi’yi güncelle;
I denklemini kullanarak hızı güncelle;
Parçacığın koordinatını güncelle;
i= i+1;
end while
end
Parçacık Sürüsü Algoritması bir başlangıç popülasyonuyla başlatılır ve algoritmanın çalışmasıyla, çözümler güncellenir ve optimum çözüm bulunmaya çalışılır. Her döngüde parçacıkların konumları, iki en iyi(best) değere göre güncellenir. Bu değerlerden ilki pbest, o ana kadar parçacığın elde ettiği en iyi çözümü sağlayan konum koordinatlarıdır. Diğer değer ise popülasyon tarafından elde edilen en iyi çözümü sağlayan konum koordinatlarıdır. Diğer değeri local en iyi(best) olarak kabul edersek, bu değer ise global en iyi olarak kabul edilir.
Aşağıda D adet parametrede oluşmuş, n adet parçacığın oluşturduğu popülasyon görülmektedir.
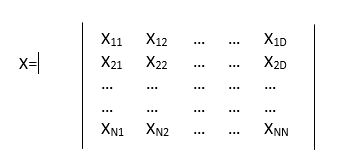
Popülasyon matrisine göre i. parçacık Xi = [ Xi1,Xi2,…,…,X1D] şeklinde ifade edilir. En iyi değeri veren parçacığın pozisyonu için de pbest şeklinde bir matris oluşturulur. Yine aynı şekilde yukarıdaki denklemde verilen hız parametresi de vektörle ifade edilir.
Denklemler de geçen C değerleri öğrenme faktörleridir. Bu değerler her parçacığı en iyi konuma çeken stokastik hızlanma terimlerini ifade eden sabitlerdir. İlk c değeri parçacığın kendi tecrübesine göre hareket etmesini, diğeri ise sürüdeki diğer parçacıkların tecrübelerine göre hareket etmesini sağlar. Bu sabitlerin değerleri belirlenirken dikkat edilmelidir. Düşük değerler seçilmesi durumunda hedefe doğru dolaşarak gider, böylelikle farklı yerler gezilerek, farklı kaynak bulma imkanı doğabilir. Fakat bu durum hedefe ulaşma süresini uzatır. Bu değerlerin yüksek seçilmesinde ise hedefe doğru hızla gidilir fakat bu durumun, hedefin atlanıp geçilmesine de sebep olabileceği unutulmamalıdır. Yapılan çalışmalar sonrasında elde edilen verilere göre en uygun c değerleri 2 olarak bulunmuştur. Ayrıca denklemde bulunan rand değerleri [0,1] arasında düzgün dağılımı rastgele değerlerdir. Denklemlerde geçen k değerleri ise iterasyon sayısını bildirmektedir.
PARÇACIKLARIN HIZ VE KOORDİNATI
Parçacıkların hız ve koordinat hesaplamaları yukarıda verdiğim I ve II numaralı denklemler ile yapılmaktadır. Yeni konum yeni hız ve bir önceki koordinat bilgisiyle hesaplanmaktadır. İkinci denklem bunu göstermektedir. x(k+1) bir sonraki koordinat bilgisi, mevcut koordinat bilgisi x(k) ile parçacığın o andaki hızı ile toplanarak bulunmakta.
İlk denklem ise mevcut hızı hesaplamaktadır. c1 ve c2 değerleri global en iyiye gidiş için önem arz etmektedir. Bu yüzden dikkatli seçilmelidir. Daha önce bahsettiğim gibi bu değerler genelde 2 seçilirler.
Yukarıda görüldüğü üzere verilen hız denklemi pbest ve gbest değerlerine bağımlıdır. Bu yüzden tüm elemanlar hesaba katılmamaktadır. Bu yüzden formülü aşağıdaki şekildeki gibi de kullanabiliriz. Bu şekildeki kulanım sayesinde yeni hız bulunurken sadece en iyilerin kullanımından kurtarılmış olacaktır. Formüldeki x değeri orantı sabiti, qi değeri ise pbest değerlerinin ağırlıklı toplamı olarak kullanılmaktadır.
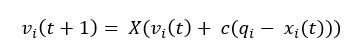
Parçacık Sürüsü Optimizasyonu Algoritması’nda bir diğer önemli nokta da komşuluk seçimidir. Üzerinde çalıştığımız probleme göre komşuluk seçimi stratejisi belirlenir. Komşuluk seçimi için genel olarak kullanılan birkaç metod vardır.
KAYNAKLAR
- Particle Swarm Optimization and Differential Evolution Algorithms: Technical Analysis, Applications and Hybridization Perspectives
- Parçacık Sürüsü Optimizasyon Algoritması ve Benzetim Örnekleri – Seçkin Tamer-Cihan Karakuzu
- Parçacık Sürü Optimizasyonunda Yeni Bir Birey Davranış Biçimi Önerisi – Ö.Tolga Altınöz-A.Egemen Yılmaz
- http://www.swarmintelligence.org
- http://wikipedia.org