- SINGLE PERCEPTRON MODEL
Multilayer Perceptrom Model’den önce Perceptron Model’den bahsetmek gerekiyor. Perceptron Model bir Yapay Sinir Ağları modelidir ve bugünkü Yapay Sinir Ağları için önemli bir temel oluşturmaktadır. Supervised (denetimli) bir training (öğrenme) algoritmasıdır. Yani ağa hem giriş hem de çıkış kümesi verili ve öğrenme beklenir. Perceptron Modeli’nde en önemli faktör eşik değeridir. Bu değer kullanılarak güzel bir sınıflandırma yapılabilmektedir. Saptanacak olan eşik değeri probleme göre belirlenebilir. Bu modelde iterasyon sayısı artırılarak öğrenme derecesi artırılabilir. Tek Katmanlı Algılayıcı’lar aşağıdaki şekilde modellenmiştir.
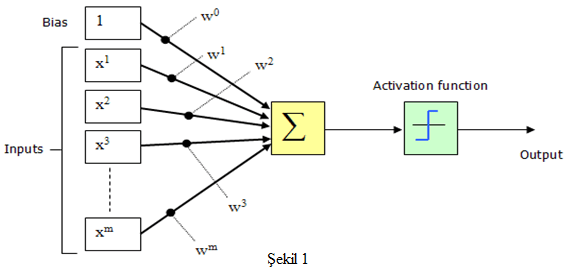
Modelde görülen x değerleri girişleri, w değerleri ise ağırlıkları ifade edilmektedir. BIAS değeri ise öğrenmeyi güçlendirmek için kullanılır. Ayrıca öğrenmeyi güçlendirirken yerel optimum değerler takılmayı da önler. Bu modelin algoritma adımlar şu şekildedir;
Adım 1) Tüm ağırlıklara başlangıç değerleri atanır. Öğrenme katsayısına küçük bir değer verilir. (Örn: Bias = 0)
Adım 2) Adım 3 ile 7 arasını belirli bir iterasyon sayısına ulaşılıncaya kadar tekrarla.
Adım 3) Her bir girdi için Adım 4 ile 6 arasını tekrarla.
Adım 4) Girdi değerlerini girdiden al.
Adım 5) Perceptron’a gelen toplam sinyali hesapla. Aktivasyonu hesapla.
Adım 6) Eğer hesaplanan değer beklen değerden farklı ise, hesaplama yanlıştır. Ağırlıkları güncelle.
Adım 7) Döngü sonunu kontrol et.
Şekil-1’de görüldüğü üzere Perceptron Model tek katmanlıdır. Bu yüzden Single Perceptron Model de denmektedir. Sadece giriş ve çıkış katmanı bulunmaktadır. Net girdi hesaplanır. Girdi eşik değerin altındaysa 0, üstündeyse 1 olarak çıkış değeri belirlenir. Çıkış beklenen değerden farklı ise ağırlık güncellemesi yapılır. Şöyle ki ; Eğer çıkış 1 bekleniyorken, 0 olarak alınmışsa ağırlıklarda artırılmaya gidilir. Tersi durumda ise ağırlıklar azaltılır. Artırım ve azaltım belirlenen delta değeri ile yapılır. Tüm eğitim seti için doğru sonuçlar bulunana kadar algoritma devam ettirilir. Her biri için doğru sonuçlar bulunduğunda öğrenme tamamlanmış sayılır. Bu modelde elde edilen çıktı fonksiyonu doğrusaldır. Perceptron Modeli ile ağa gösterilen örnekler iki sınıf arasında paylaştırılarak iki sınıfı birbirinden ayıran doğru bulunmaya çalışılır. Aşağıda örnekle gösterilmiştir.
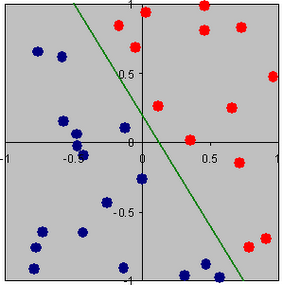
Şekil-2
Şekil-3
- DOĞRUSAL AYRILABİLİRLİK (Linear Seperability)
Bir düzlemde sadece bir hat varsa iki sınıfa ait iki boyutlu örüntülerin bir kümesi doğrusal olarak ayrılabilirdir. Şekil-2’de görülen doğru düzlemi bir hatla ikiye ayırmıştır. Verilen düzlemdeki örneklerin hepsi iki gruptan birine dahil olmuştur. Yani problem çözülebilir. Konuya örnek olarak and ve or fonksiyonları verilebilir. Bunları şekil üzerinden görelim. Yandaki şekilde veya fonksiyonu gösterilmiştir. Bilindiği üzere or fonksiyonunun 1 çıkışı vermesi için giriş değerlerinden birinin bir olması yeterli olur. Bu durumda or fonksiyonunun çıktılarını düzlemde iki gruba ayırmak istersek yandaki şekilde bu işlemi gerçekleştirebilir. Yani or fonksiyonu doğrusal ayrılabilirdir. Or fonksiyonunu yapay sinir ağları yöntemleriyle sisteme öğretmeye çalışırsak başarılı olabiliriz. Aynı durum and fonksiyonu içinde geçerlidir. Tek farkı doğru farklı yerden geçip düzlemi ikiye ayıracaktır. Eğer bir problem doğrusal ayrılabilir ise o zaman Perceptron Öğrenimi ile örüntülerin bir kümesinden ağırlıklar elde edilebilir. Eğer problem doğrusal ayrılabilir değilse Single Perceptron Modeli ile çözüme ulaşamayız.
- XOR PROBLEMi
Xor fonksiyonu doğrusal ayrılabilir değildir. Daha önce bahsettiğimiz or ve and fonksiyonunun çıktılarını düzlemde iki gruba ayırabiliyorduk. Fakat xor fonksiyonunda bunu gerçekleştiremiyoruz. Düzlemdeki çıktıları tek bir hatla ikiye bölemiyoruz.(Şekil 5) En az iki doğru gerekiyor. Xor problemi Yapay Sinir Ağları’nın “Hello World”ü olarak bilinir. Perceptronlar XOR Problemi gibi doğrusal olarak sınıflandırılamayan problemleri çözümünde başarısızdır. XOR Problemi’ni çözmek için geriye yayılımlı çok katmanlı ağlardan faydalanılabilir.
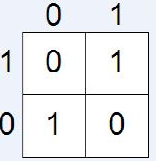
Şekil-4
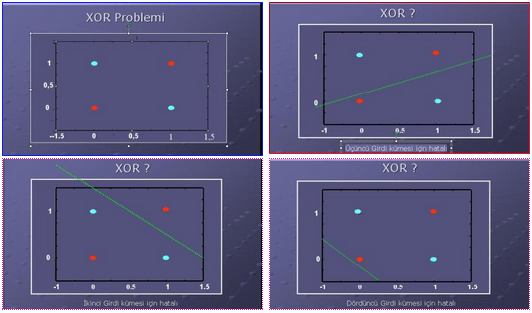
Şekil-5
- MULTI-LAYER PERCEPTRON MODEL
Çok Katmanlı Algılayıcılar (MLP) XOR Problemi’ni çözmek için yapılan çalışmalar sonucu ortaya çıkmıştır. Rumelhart ve arkadaşları tarafından geliştirilen bu modeli ‘Back Propogation Model’ yada hatayı ağa yaydığı için ‘Hata Yayma Modeli’ de denmektedir. Delta Öğrenme Kuralı denilen bir öğrenme metodu kullanır. MLP özellikle sınıflandırma ve genelleme yapma durumlarında etkin çalışır. Çok Katmanlı Ağ’ların yapısı aşağıdaki gibidir.
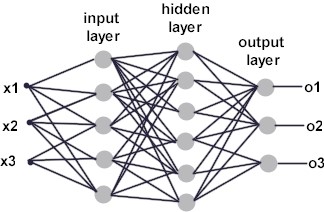
Şekil-6
Birçok giriş için bir nöron yeterli olmayabilir. Paralel işlem yapan birden fazla nörona ihtiyaç duyulduğunda katman kavramı devreye girer. Görüldüğü üzere Single Perceptron Model’den farklı olarak arada gizli(hidden) katman bulunmaktadır. Giriş katmanı gelen verileri alarak ara katmana gönderir. Gelen bilgiler bir sonraki katmana aktarılırlar. Ara katman sayısı en az bir olmak üzere probleme göre değişir ve ihtiyaca göre ayarlanır. Her katmanın çıkışı bir sonraki katmanın girişi olmaktadır. Böylelikle çıkışa ulaşılmaktadır. Her işlem elemanı yani nöron bir sonraki katmanda bulunan bütün nöronlara bağlıdır. Ayrıca katmandaki nöron sayısı da probleme göre belirlenir. Çıkış katmanı önceki katmanlardan gelen verileri işleyerek ağın çıkışını belirler. Sistemin çıkış sayısı çıkış katmanında bulunan eleman sayısına eşittir. Single Perceptron Modeli incelerken bahsettiğimiz nöron yapısı burada aynen geçerlidir.
Modelde aktivasyon fonksiyonu olarak herhangi bir matematiksel fonksiyon kullanılabilir. Ancak Sigmoid, tang, lineer, threshold ve hard limiter fonksiyonları en çok kullanılan fonksiyonlardır.
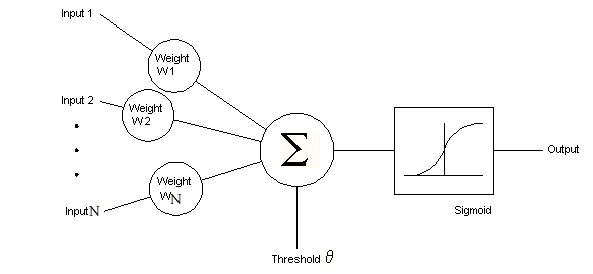
Şekil-7
Çok katmanlı ağlardaki hücreler yandaki gibidir. Aktivasyon fonksiyonu olarak yandaki modelde sigmoid fonksiyonu seçilmiştir. Çok katmanlı ağda öğrenme Delta Öğrenme Kuralı tabanlıdır. Ağın öğrenebilmesi için örnek giriş ve çıkışlardan oluşan eğitim seti şarttır. Geri Yayılımlı Yapay Sinir Ağları’nda öğrenme işlemi bir anlamda örnek setindeki giriş değerleriyle, çıkış değerlerini eşleştiren fonksiyonu bulma işlemidir. Sistemin öğrenme metodu genel olarak iki aşamadan oluşur. Birinci kısım ileri doğru hesaplamadır. İkinci kısım ise geri doğru hesaplamadır (back propogation).
İleri doğru hesaplama aşamasında sisteme verilen girdi ara katmanlardan geçerek çıkışa ulaşır. Her işlem elemanına gelen girdiler toplanılarak net girdi hesaplanır. Bu net girdi aktivasyon fonksiyonundan geçirilerek mevcut işlem elemanının çıktısı bulunur. Ve bu çıktı değeri bir sonraki katmanda bulunan işlem elemanlarına gönderilir. Bu işlemler tekrar edilerek en son çıktı katmanından çıktılar elde edilir. En çok kullanılan aktivasyon fonksiyonu olan sigmoid fonksiyonu şekildedir.
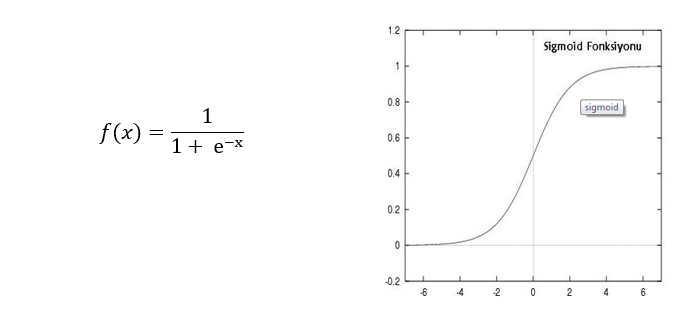
Şekil-8
Ağdan çıktı alınmasıyla öğrenmenin ilk aşaması bitirilmiş olur. İkinci aşama hatanın dağıtılması olacaktır. Beklenen çıktı değeri ile elde ettiğimiz birbirinden farklı ise hata vardır. Geriye doğru hesaplama aşamasında hata ağırlık değerlerine dağıtılarak her iterasyonda azaltılması beklenir. Sisteme başlangıçta random olarak verilen ağırlık değerleri, hataların ağırlıklara dağıtılmasıyla her iterasyonda güncellenmiş olur.
Genelleştirilmiş Delta Öğrenme Kuralı’nın yapısı genel olarak aşağıdaki gibidir.
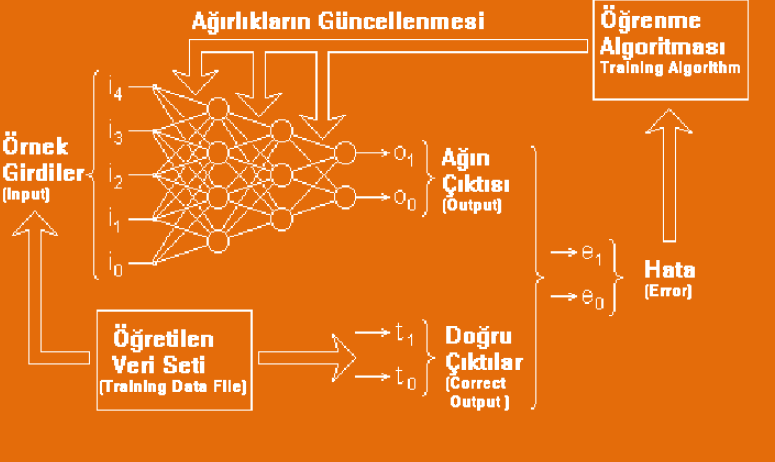
Şekil-9
Multi-layer Perceptron(MLP) yani Çok Katmanlı Algılayıcılar, Yapay Sinir Ağları’na olan ilgiyi hızlı bir şekilde artırmıştır. MLP ile birlikte YSA tarihinde yeni bir dönem başlamıştır. Geniş kullanım alanına sahiptir. Örnek verecek olursak; Otomotiv alanında yol izleme, rehberlik vs. gibi konularda kullanılmaktadır. Bankacılıkta kredi kartı suçu tespiti ve kredi uygulamalarında kullanılmaktadır. Uzay sanayinde uçuş simülasyonu ve otomatik pilot uygulamalarında kullanılır. Finans sektöründe ise döviz kuru tahminlerinde kullanılır.
- MULTI-LAYER PERCEPTRON MODEL UYGULAMASI
Uygulamamızı anlatırken, sadece main sınıfımızdaki kodlar konulup bu sınıfın kullandığı fonksiyonları kod koymaksızın anlatılacaktır. Uygulamamıza giriş olarak 9 değer verilmiştir bunlar;
inputs = [ 0 0 0 ; 0 1 0 ; 1 0 1 ; 1 1 1]; targets = [ 1 1 ; -1 -1 ; -1 -1 ; 1 1]; ni = 3; nh = 4; no = 2; wsize = ((ni+1)*nh)+(nh*no); net = 4*rand(1,wsize)-2; ci = zeros(ni+1,nh); co = zeros(nh,no);
Giriş değişkenlerimize sırasıyla bakacak olursak;
inputs,targets: Multi Layer Perceptron modeli danışmanlı öğrenme yöntemini kullanarak algoritmanın eğitimini gerçekleştirir. Danışmanlı öğrenme modelinde ise algoritmanın eğitilmesi için giriş değerleri ve bu giriş değerlerden üretilmiş olan çıkış değerleri verilmelidir. Uygulamamızdaki giriş ve çıkış değerleri raporumuzda açıklanan ex-or problemi ile benzerlik göstermektedir. Böylece Multi Layer Perceptron modelinin “Hello word” ü olarak tanımlanan bir uygulamayı gerçekleştirmiş oluyoruz.
ni: Bu değişken algoritmamızda giriş sayısı olarak kullanılmaktadır. Bu değişkenin değiştirilmesi halinde inputs değişkenin içerisinde bulunan değerleri de değiştirmemiz gerekecektir.
nh: Bu değişken ise ara katmandaki nöron sayısı olarak tanımlanmaktadır.
no: Bu değişken ise targets değişkenine bağlıdır ve girişler sonucunda üretilen çıkış sayısıdır. Eğer targets sayısı değiştirilirse bu değişkeninde değiştirilmesi gerekmektedir.
wsize : bu değişken giriş sayısı, nöron sayısı ve çıkış sayısı kullanılarak oluşturulan ve ağırlık sayısını temsil eden değerdir. Denklemde kullanılan (ni+1) değerindeki +1 öğrenmeyi güçlendirmek için kullanılan bias değeridir.
net: Bu değişken ağırlıkların tutulduğu vektördür. Başlangıçta rastgele atanan değerler ile doldurulur ama kullanılan algoritmada her bir döngüde bu değerler çeşitli parametrelere göre değiştirilmektedir.
ci: Her döngüde girişlerde oluşan değişimi tutan vektördür. Başlangıç değeri olarak giriş sayısı ve ara katman sayısı parametrelerine göre sıfır değerleri atanır. Değişim oldukça bu vektör düzeltilir. Denklemde kullanılan (ni+1) değerindeki bias değeri için kullanılmıştır.
co: Bu vektör ise çıkış değerlerindeki değişimleri tutmaktadır. Başlangıç değerleri ara katman sayısı ve çıkış sayısı parametrelerine göre sıfır olarak atanır. ci,co değişkenleri hatanın hesaplanması için kullanılmaktadır. Böylece her adımda hata kontrolü yapabiliyoruz ve bu hata kontrolüne göre eğitimi durdurabiliyoruz.
for i=1:1000 error = 0; for j=1:4 [ net,co,ci,err ] = BackProp(net,inputs(j,:),targets(j,:),ni,nh,no,co,ci ); error = error + err; end if mod(i,100)==0 display([' Error ',num2str(error)]) end end
Bu kod bloğu eğitim gerçekleştiği yerdir. Bizim uygulamamızda belli bir iterasyon sayısı boyunca eğitim devam etmektedir ve bin iterasyonda sonlanmaktadır fakat bu yaklaşım yerine her adımda hesapladığımız hata değerini(gerçek değere yakınlığını) de kullanabiliriz. Yani algoritmamız bizim belirlediğimiz hata değerinden küçük oluncaya kadar eğitime devam edebilir.
Algoritma her bir iterasyonda her bir giriş için:
BackProp(net,inputs(j,:),targets(j,:),ni,nh,no,co,ci ); fonksiyonunu kullanmaktadır. Bu fonksiyon parametre olarak ağırlık değerleri, girişler, çıkışlar, giriş sayısı, nöron sayısı, çıkış sayısı ve hata hesaplamaları için kullanılan parametreler alarak işlemini gerçekleştirmektedir. İlk önce ileri doğru hesaplama gerçekleştiriliyor. Bu hesaplama iki kısma ayrılıyor. Birincisi giriş katmanı ile ara katman arasında, ikincisi ise ara katman ve çıkış katmanı arasında gerçekleşiyor. İkinci kısım birinci kısımdan çıkan değerleri kullanmak suretiyle çıkışlar üretiliyor. İleri doğru hesaplama yapılırken birçok aktivasyon fonksiyonu kullanılabilir. Bizim uygulamamızda hiperbolik tanjant fonksiyonu kullanılmaktadır. Böylece ileri doğru hesaplama tamamlanmış oluyor. İleri doğru hesaplama tamamlandıktan sonra ağa sunulan girdi için ağın ürettiği çıktı ağın beklenen çıktıları ile karşılaştırılır. Bunların arasındaki fark hata olarak kabul edilir. Bu hata, ağın ağırlık değerlerine dağıtılarak bir sonraki iterasyonda hatanın azaltılması sağlanır. Algoritma eğitimi de sürerken toplamda on adımda hata yazdırılarak hatanın giderek azaldığı gösterilmiştir. Böylece hata azaltılarak bütün ağa paylaştırılmış ve geri doğru hesaplama tamamlanmıştır. İki aşama da sona erdikten sonra eğitim tamamlanmış ve değerlerin test edilmesi aşamasına gelinmiştir.
for j=1:4 output = EvalNN( inputs(j,:),net,ni,nh,no ); display([' Inputs [',num2str(inputs(j,:)),'] --> outputs: [',num2str(output),']']) end
Bu kod bloğunda kullanılan EvalNN( inputs(j,:),net,ni,nh,no ); fonksiyonu ile giriş değerleri test edilmektedir ve öğrenmenin ne kadar başarılı olduğu belirlenmektedir. Test aşamasından çıkan sonuçlar ise şöyledir.
inputs = 0 0 0 0 1 0 1 0 1 1 1 1 targets = 1 1 -1 -1 -1 -1 1 1 Error 2.0021 Error 1.9997 Error 0.012925 Error 0.0028741 Error 0.0016513 Error 0.0011705 Error 0.00091238 Error 0.00075076 Error 0.00063978 Error 0.00055868 Inputs [0 0 0] --> outputs: [0.99643 0.99213] Inputs [0 1 0] --> outputs: [-0.98962 -0.98221] Inputs [1 0 1] --> outputs: [-0.99356 -0.98541] Inputs [1 1 1] --> outputs: [0.98985 0.98393]
Görüldüğü üzere hata gittikçe azalmıştır ve girilen giriş değerlerine göre ağın ürettiği çıkış değerleri gerçek değerlere çok yaklaşmıştır.
KAYNAKLAR
- Matlab Neural Network Toolbox
- http://tr.wikipedia.org
- http://members.comu.edu.tr/boraugurlu/courses/bm434
- Özgür ÖZDEN tez çalışması.
- http://www.zinderud.com
- http://ube.ege.edu.tr/~cinsdiki/UBI521/Chapter-1/cinsdikici-neural-net-giris.pdf