Shortest Path Problem – En Kısa Yol Problemi

Bir Cevap Yazın

Shortest Path Problem yani En Kısa Yol Problemi’nden önce bu konuyla ilgili olan Graph Theory’den bahsetmek istiyorum.

Graph Theory

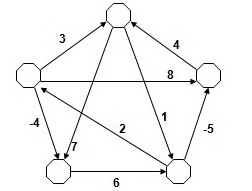
Graf Teori yani Çizge Kuramı, çizgeleri yani grafları inceleyen matematik dalıdır. Graflar node (yada vertice) yani düğümler ve edge yani bağlantılardan oluşan bir çeşit ağ yapısıdır. Bağlantıların her birinin değeri vardır ve tek yada çift yönlü olabilirler. Bir G grafı, G = (V,E) şeklinde ifade edilir. Burada V düğümler kümesi , E ise bağlantılar kümesini ifade eder.

Shortest Path Problem

Shortest Path Problem, Graph Theory içerisinde önemli bir problemdir. Graf içerisinde belirtilen node’lar arasındaki en kısa yolu bulmayı amaçlar. Bu özelliğiyle Gezgin Satıcı Problemi’ne de (Travelling Salesman) benzer. Ancak Gezgin Satıcı’dan iki noktada ayrılır. Birincisi, hedef düğüme giderken tüm düğümlere uğramak zorunda değiliz. İkincisi de hedefe vardıktan sonra başlangıca dönmüyoruz.

En kısa yollar döngüler içeremez, ancak negatif bağlantı değerleri bulundurabilirler. Bununla birlikte n tane düğümün olduğu bir grafta en kısa yol n-1 kenardan daha fazla kenara sahip olamaz.

Kaynak nodun diğer tüm node’lara olan en kısa yollarını bularak Graph Theory içerisinde yer alan En Kısa Yol Ağacı’nı da (Shortest Path Tree) oluşturabiliriz.

Shortest Path Problemleri

· Single-Source (Single – Destination) : Verilen bir node’dan diğer tüm node’lara olan en kısa yolun bulunması problemidir.

  • Single-Pair: Verilen iki node arası en kısa yolun bulunması problemidir.
  • All-Pairs : Grafta bulunan tüm ikililer arası en kısa yolun bulunması problemidir.

En Kısa Yol Problemi’nin Görüldüğü Yerler

En Kısa Yol Problemi’ni çözen çeşitli algoritmalardan daha sonra bahsedeceğiz, ancak daha önce bu problem nerelerde görülür onlardan bahsetmek istiyorum.

  • Navigasyon cihazlarında güzergah ayarlaması sırasında
  • Dynamic Routing kullanan Network’lerde En ucuz yada hızlı hat ayarlaması yaparken
  • Limancılık, havacılık, postacılık güzergah ayarlaması esnasında
  • Hatta Rubik Cube’ü en az hamlede çözmek için dahi kullanılabilir.
  • Robot hareket planlaması

Kaynaklar

Bugün 1, bugüne kadar toplam 408 kez ziyaret edildi.

Benzer Yazılar:

Bir yanıt yazın

E-posta adresiniz yayınlanmayacak. Gerekli alanlar * ile işaretlenmişlerdir